Maker Faire 2013
Hands-on quantum optics: Lasers, detectors, entangled pairs

It's time to be on the road again for experimental people working at the Centre for Quantum Technologies. This year, we flock around at Singapore Mini Maker Faire at the *SCAPE warehouse on 27 July and show some of the basic tools & toys we use and often make in our labs. Similar to earlier events, we demonstrate live and without a safety net some of the weird aspects of quantum physics: light can show aspects both of waves and particles, and, if several distinguishable particles come into play, entanglement becomes important.

This web page gives you a few more details to entangled pair experiment shown in the exhibit because we figured we better write down some of the stuff.

The idea and its history

1935: The origins and the paradox of Einstein, Podolsky and Rosen

One of the main ingredients of the then newly developed quantum theory was the superposition principle, stating that a system can be in a well-defined superposition of several states. This was found to be necessary to describe states of simple degrees of freedom, like the position of an electron in an atom, thereby explaining e.g. their spectral lines.

However, that principle should hold also for more complex states, like a two-particle state, where the two particles can be separated by a large distance. In such a scenario, no particle is in a well-defined state on its own, but the whole system is. Such states of a system were named "entangled states".

For some of these states, quantum physics predicts a correlation of measurement results on both particles or locations, but random outcomes of measurements on each side. The argument of Einstein, Podolsky and Rosen (EPR) in 1935 [1] then was that such a combination seems to violate common sense, where one assumes that a measurement should reflect an existing physical property ("Elements of reality") which is somehow localized in an area where the particle resides and the measurement is carried out. This idea is referred to as "local realism". A connection with something very far away seemed to violate the concept that information on what a measurement outcome is can only travel with the speed of light, and that in a properly conducted observation there cannot be any randomness. By postulating that "local realism", EPR therefore concluded that the newly developed quantum theory must be incomplete.

1964-1974: A quantitative test evolves

By looking at a quantum system of two particles in a certain entangled state, John S. Bell was able to cast the assumingly reasonable demand of local realism into a mathematical form [2]. With this formalism, Bell could give a strict bound on a combination of a correlation of measurement results, which is now referred to as a Bell inequality. Quantum physics, on the other side, would predict correlations which violate Bell's inequality. Thus, the foundations were set to carry out a measurement which could distinguish between the local realistic models, and the quantum physics prediction.

In the following few years, John Clauser, Mike Horn, Abner Shimony, and Richard Holt came up with a specific physical system to test this inequality in a realistic experiment [3]. It is the basis of many modern tests of Bell's inequalities, and was referring to pairs of particles with a simple spin-1/2 property. That could be electronic or nuclear magnetic spins of a particle pair, but the concept also applies to the polarization of a photon pair.

In the Dirac notation, the polarization state |H_1,2⟩ denotes a horizontal, and |V_1,2⟩ a vertical polarization of photon 1 and 2, respectively. The superposition states

|+⟩ = 1/√2 (|H⟩ + |V⟩) and |-⟩ = 1/√2 (|H⟩ - |V⟩)

correspond to +45° and -45° diagonal linear polarizations.

A prominent entangled quantum state of a photon pair is the so-called singlet state, which in this notation can be written as

|Ψ^-⟩ = 1/√2 (|H₁V₂⟩ - |V₁H₂⟩) .

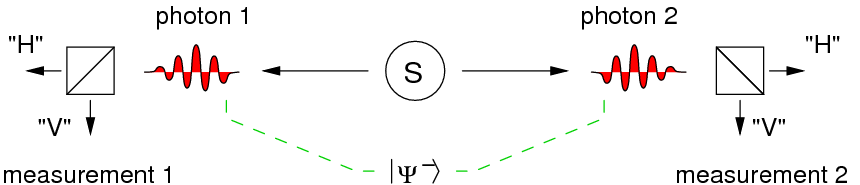
In a measurement which distinguishes horizontal and vertical polarization, this state would either lead to a result with photon 1 in horizontal and photon 2 in vertical, or with photon 1 in vertical and photon 2 in horizontal polarization: The measurement results are always opposite on both sides.

This also holds if a measurement is carried out that distinguishes ±45° diagonal polarizations, since

|Ψ^-⟩ = 1/√2 (|+₁-₂⟩ - |-₁+₂⟩) .

For both H/V and ±45° measurements, the results on both sides are anti-correlated.

Correlation functions

In a real experiment, one would get either one of two possible outcomes on each side, for example H or V on one side, and + or - on the other side if a measurement apparatus distinguishes ±45° polarizations. For measurements on many pairs, one would get a number of events N_H,+, N_V,+, N_H,-, and N_V,- for all possible combinations. From this, one can define a correlation function

E_HV,± := (N_H,+ + N_V,- - N_H,- - N_V,+) / N_T,

with a total event number N_T = N_H,+ + N_V,- + N_V,- + N_H,- .

This correlation function can only take values between between -1 and +1. For the singlet state and the same measurements on both sides, the anti-correlation quantitatively reads E_HV,HV = E_±,± = -1.

A correlation function can not only be defined for measurements H/V or ±45°, but for an arbitrary rotation angle φ with respect to the H/V directions.

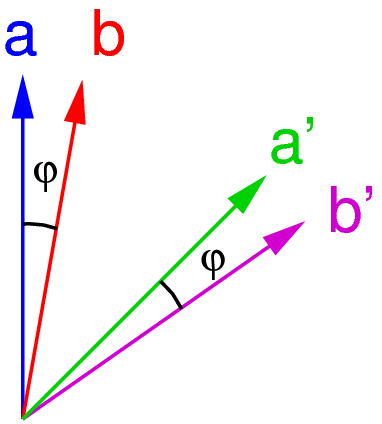
The quantitative version of the Bell inequality now makes two choices of measurement orientations on the two sides; we refer to them as a and a' on one side, and b and b' on the other side. Correlation functions corresponding to these orientations ("settings") are combined to a new quantity:

S := E_a,b - E_a',b + E_a,b' + E_a,b'

With the argument of J.S. Bell, under the assumption that there is a local realistic model with "hidden" parameters determining the measurement outcomes, this quantity is bounded - expressed by the inequality

|S| ≤ 2.

Quantum physics, on the other side, allows to calculate the expectation values of these correlation functions for a given state of the photon pairs. For a choice of settings a=H/V, a'=±45°, and settings b and b' rotated by an angle φ with respect to a and a', the singlet state |Ψ^-⟩ leads to a value of S shown below:

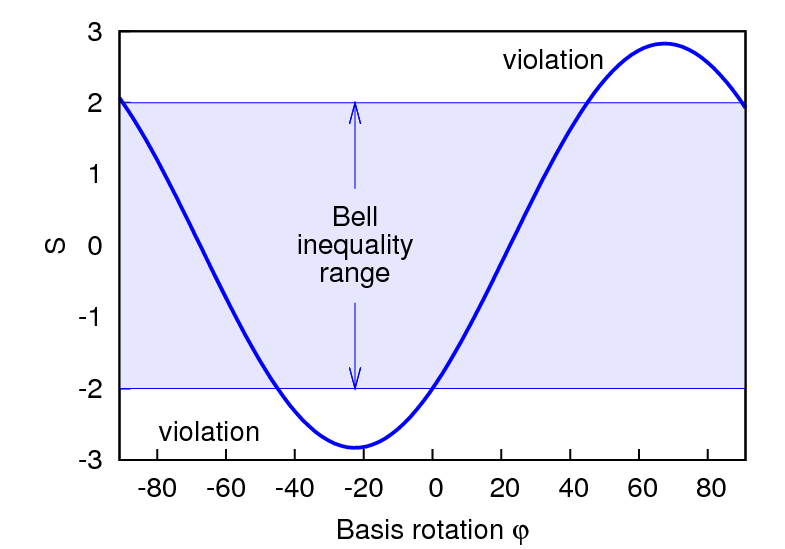
For some angles φ, S is out of bounds fixed by the Bell inequality. A measurement of polarization correlations for a proper relative orientation φ between the two sides should therefore probe the local realistic assumption behind the Bell inequality.

1982: Aspect's experiment with atomic cascades

The first convincing experiment to test a Bell inequality was carried out by Alain Aspect and coworkers [4]. They used an optical decay cascade in excited calcium atoms to prepare photon pairs in the singlet polarization state. After collecting data over a measurement time of xxx hours, the team found a violation of the Bell inequality of yyy standard deviations. For the first time, all simple local realistic models for measurement outcomes on this combined system of two photons could be shown not to predict the observations.

1995: Bright photon pair sources based on parametric conversion

Photon pairs with a strong correlation in time can not only be prepared from cascade decays in atoms, but also in a nonlinear optical process called parametric down conversion. In appropriate materials, photons from a strong light field can be "broken up" into pairs of photons of lower energy, as long as the total energy and, depending on the boundary conditions, the total momentum is conserved.

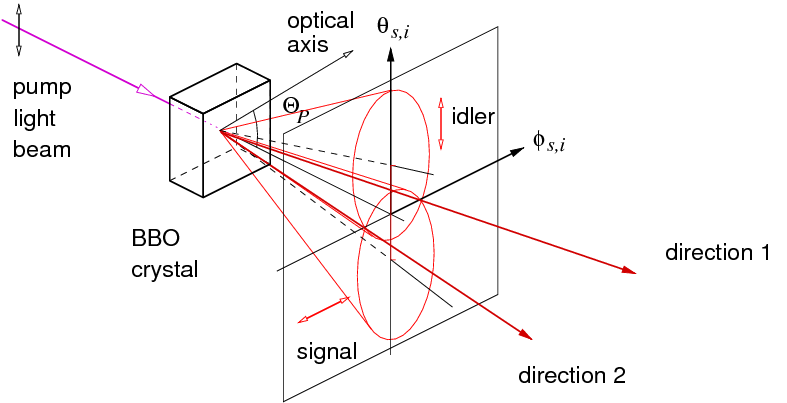
While this process has been known for over two decades, Paul Kwiat and coworkers in 1995 used it to prepare in a clever way photon pairs into the singlet state suitable for testing the Bell inequality with a much higher statistical confidence [5]. By now, this type of source can be engineered to prepare photon pairs in a singlet state with an extremely high precision.

A modern experiment

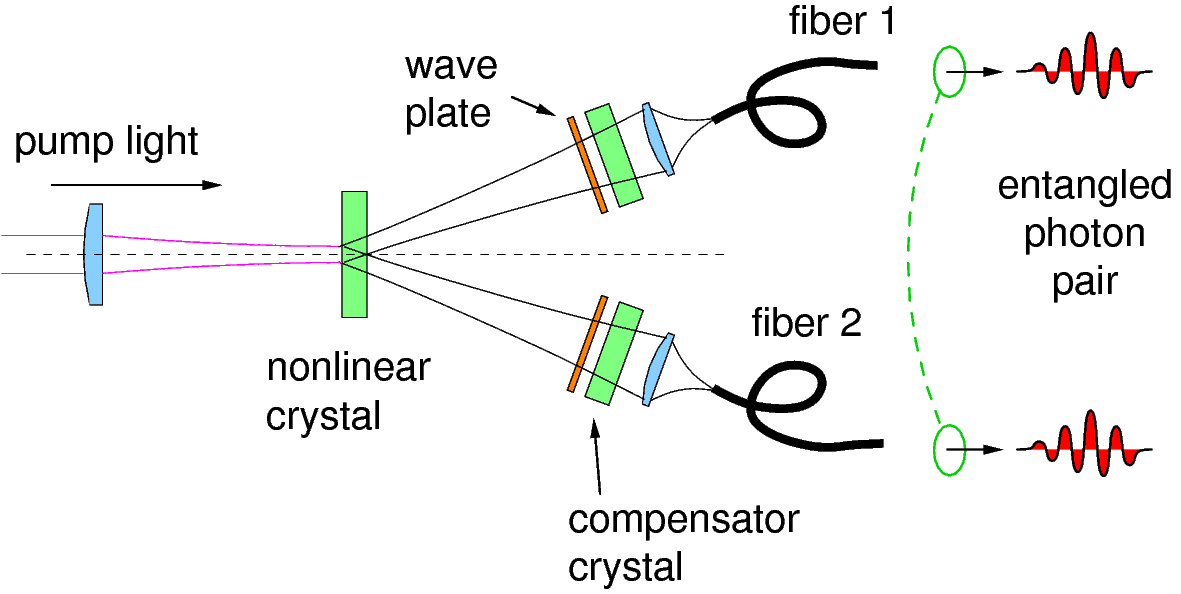
Fiber-coupled pair source

Entangled pair sources have seen a dramatic improvement in the last few years; light is now generated into optical fibers, and can be conveniently transported [6]. They also help to block unwanted light:

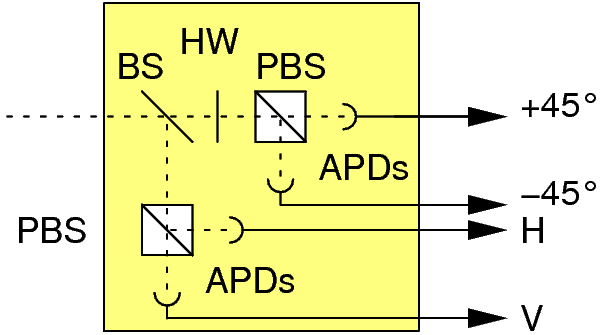
Photodetection with avalanche photodiodes

The polarization of photons can be measured by a combination of beam splitters (BS), polarizing beam splitters (PBS) and half wave plates (HW), which divert an incoming photon onto one of four avalanche photodetectors. Those devices give a discrete arrival signal for incoming photons with a probability ("quantum efficiency") of about 50%.

What can you do at the exhibit?

Observe down conversion

We bring along an entangled photon pair source which was used in a number of quantum key distribution experiments [8]. You can easily identify the components necessary to make these pairs - including a blue pump laser, similar to those built in to blu-ray disc players.

We count photons coming out of this source one by one, but this does not mean that they are too weak to be seen: Check out for yourself that you can see the photons, and be assured that for each photon you see coming from the conversion crystal, there is a twin brother going into a different direction - and with an energy to make up for the blue pump photon destroyed for their creation.

What you have to do is to look through the yellow window, close to the arrow tip, and look into the centre of the crystal. If you move your eye around a little, you see the colors changing, revealing energy and momentum conservation.

Change orientation of detector basis

Photos transport their polarization along fibers following the layout the fiber in a particular way - depending to the fiber orientation, this may alter the polarization plane, and thus allow to orient the measurement basis such that the photon pair in the singlet state actually violate a Bell inequality. Additionally, the looping of optical fiber can make elliptical polarization due to birefringence.

We have a number of such fiber loops curled up in paddles, which can be oriented with respect to each other by turning corresponding handles. This way you can choose the measurement orientation of one of the detectors - and to hit a condition where you are able to violate a Bell inequality!

See how strongly you can violate the Bell inequality yourself

No worries - it's ok to violate the Bell inequalities - even in Singapore! There are no fines associated with it - after all, they just follow of one particular model of how people thought nature can be explained. And finding out if such an explanation holds is at the very core of what scientists do to improve on our understanding of the world.

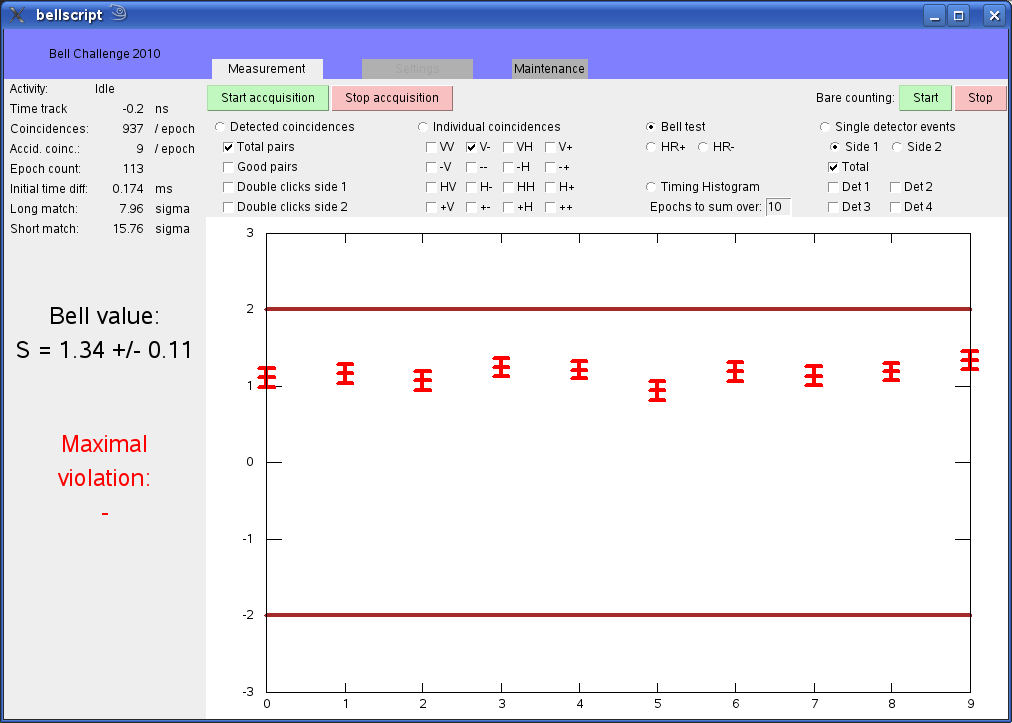
In the exhibit, you can align the measurement directions by adjusting the handles such that you will see various values for the correlation value S. If the conditions are right, you will get a result which lays outside the bounds given by the Bell inequality. But careful: These measurements are carried out not on an infinite number of photon pairs, but at a few 1000 only, distributed over the various combination of results. As a consequence, you will get a range of uncertainty for the Bell inequality.

Such an uncertainty is very common on every measurement you take, and you need to think of the consequences what this has. One aspect of it is that you can not exclude for sure that the local realistic model holds, but only with a certain statistical confidence. This, however, is VERY high even for the measurements you can carry out yourself.

Just to document you effort, we will show you how to take this measurement, and sign a certificate with your measurement result!

What is this good for?

Entangled photon pairs are at the core of many recent physical applications of quantum information technologies, which try to make use of entangled states for novel and secure communication or measurement schemes. They also help in basic science research, allowing to gain a better understanding of nature.

Secure communication

In 1991, Artur Ekert suggested to use the entanglement in a singlet photon pair for a cryptography task [7], making use the "monogamy of entanglement". This states that someone who wants to interfere with a communication between two parties with entangled photons will reduce the entanglement. The legitimate communication partners can test how strongly their photon pair still violates a Bell inequality, and infer how much information may have leaked to an eavesdropper.

We implemented this protocol here in Singapore [8], using the actual equipment you see in the exhibition. A secure key could be generated by sending one of the photons from the pair through air with telescopes.

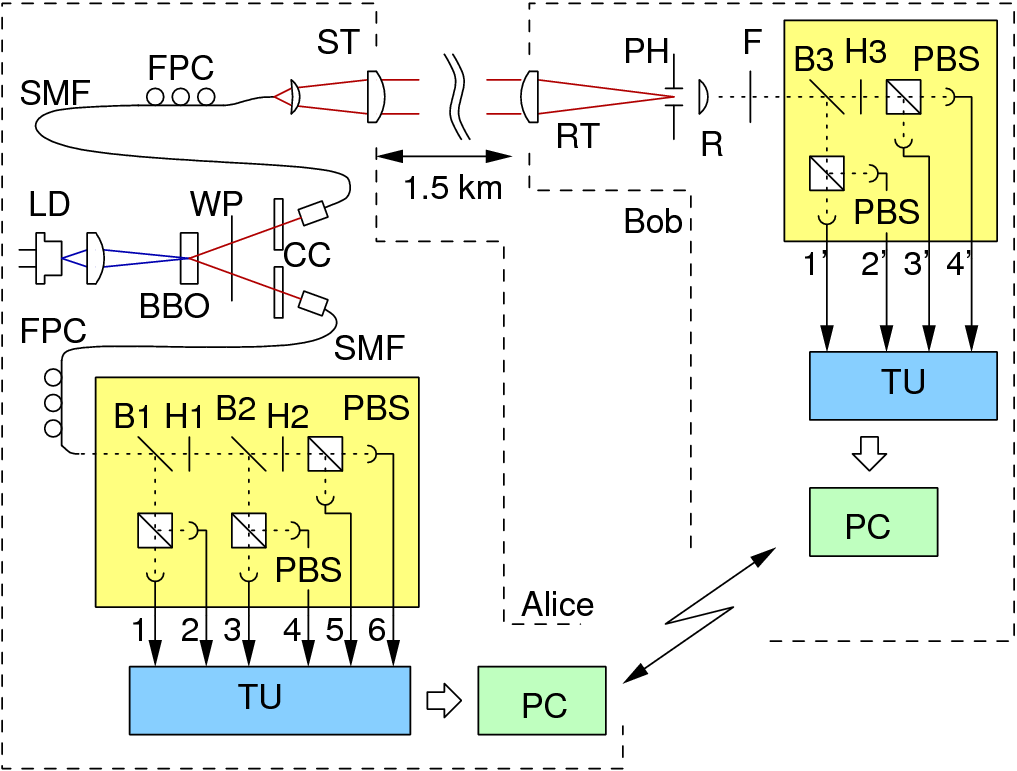
Random numbers

A key resource of secure communication, even with existing technology, are good random numbers. While it is, interestingly, not really clear what good random numbers really are, it is known what bad random numbers are: One of the things you don't want is that anyone else, say the members of an amost friendly secret service, knows or can easily guess the numbers you used for encryption.

Since a Bell test violation shows that there is nothing in nature, not even someone with a trench coat and dark sunglasses, that knows about the outcome of some measurements, these can be used as a basis for your encryption. This is one of the current active research areas at CQT.

Quantum teleoprtation

One of the more prominent applications using entangled photon pairs is referred to as quantum teleportation, where the state of a photon can be transferred to a remote location without even destroying it.

Basic science

We also use these photon pairs to carry out tests of other alternative explanations, similar in flavour of the local realistic theories. Such a a testable theory was suggested by Anthony Leggett, who often visits Singapore. We carried out this test with an advanced photon pair source, and still found that the result exceeds the bound required by the Leggett model [9]. This keeps the mystery on many aspects of quantum mechanics open, with a more things to be discovered....

(Near) future science

Loopholes

When claiming that with the experiment we can violate a Bell inequality, we should perhaps be a little be more precise: since our photodetectors don't really work with 100% efficiency, we do not see all photons of all pairs generated. This means, at the moment, we can only exclude that local realistic theories if we assume that the choice which photons are detected and which are lost is completely random.

While this seems reasonable, it still remains to be shown that this assumption is not necessary. With the recent development of very good detectors, and with some improvement on the efficiency of pair sources such as the one demonstrated in the exhibition, this should be possible in the near future: Quite a number of research groups worldwide are working on this problem right now, and progress is made in the last months in a number of groups in the world. Stay tuned, probably in the next year or two this problem will be solved!

References

[1]	A. Einstein, B. Podolsky, and N. Rosen: "Can quantum-mechanical description of physical reality be considered complete?", Physical Review 41, 777 (1935).
[2]	J.S. Bell: "On the Einstein Podolsky Rosen paradox", Physics 1, 195 (1964).
[3]	J.F. Clauser, M.A. Horne, A. Shimony, and R. A. Holt: "Proposed experiment to test local hidden-variable theories", Phys. Rev. Lett. 23, 880-884 (1969).
[4]	A. Aspect, J. Dalibard, G. Roger: "Experimental test of Bell's inequalities using time-varying analyzers", Phys. Rev. Lett. 49, 1804 (1982).
[5]	P.G. Kwiat, K. Mattle, H. Weinfurter et al., Phys. Rev. Lett. 75, 4337 (1995).
[6]	C. Kurtsiefer, M. Oberparleiter, and H. Weinfurter: "High efficiency entangled photon pair collection in type II parametric fluorescence", Phys. Rev. A 64, 010102 (2001).
[7]	A. Ekert: "Quantum cryptography based on Bell’s theorem", Phys. Rev. Lett. 67, 661 (1991).
[8]	A. Ling, M.P. Peloso, I. Marcikic, V. Scarani, A. Lamas-Linares, C. Kurtsiefer: "Experimental quantum key distribution based on a Bell test", Phys. Rev A 78, 020301 (2008).
[9]	C. Branciard, A. Ling, N. Gisin, C. Kurtsiefer, A. Lamas-Linares, V. Scarani: "Experimental Falsification of Leggett's non-Local Variable Model", Phys. Rev. Lett. 99, 210407 (2007).